Des nombres étranges dans les collisions des particules
Une connexion inattendue a émergé entre les résultats des expériences de physique et un ensemble de nombres qui concernent les mathématiques pures.
Suivez-nous sur notre page Facebook et notre canal Telegram

Traduction d’un article de Quanta Magazine par Kevin Hartnett
Au Grand Collisionneur de Hadron à Genève, les physiciens tirent des protons sur une piste de 27 kilomètres à une vitesse proche de celle de la lumière. C’est l’une plus belles expériences de physique au monde, mais quand les physiciens tentent de comprendre les résultats de ces collisions, alors ils commencent avec un outil très simple qu’on connait comme les diagrammes de Feynman et ce n’est pas très différent dont un enfant dessinerait les collisions.
Les diagrammes de Feynman ont été conçus par Richard Feynman dans les années 1940. Ce sont des lignes représentant des particules élémentaires qui convergent vers un vertex (qui représente une collision) et ces lignes dévient de ce sommet pour représenter les pièces qui émergent de la collision. Ces lignes peuvent se finir ou elles peuvent converger de nouveau. La chaine des collisions peut être aussi longue que la considération des physiciens.
À ce schéma, les physiciens ajoutent des nombres pour la masse, le momentum et la direction des particules. Ensuite, ils commencent une procédure laborieuse de comptage avec des intégrations, des additions, des élévations au carré, etc. Le résultat final est un seul nombre qu’on connait comme la probabilité de Feynman qui quantifie la chance que la collision des particules s’est produite selon les prévisions. Dans un certain sens, Feynman a inventé ce diagramme pour encoder des mathématiques complexes comme dans un appareil de comptabilité selon Sergei Gukov, un physicien théoricien et mathématicien à la California Institute of Technology.
Les diagrammes de Feynman ont servi à la physique pendant de nombreuses années, mais ils sont limités. La première limite est purement procédurale. Les physiciens produisent des collisions à des énergies de plus en plus élevées ce qui nécessite une meilleure précision. Et quand la précision augmente, la complexité des diagrammes de Feynman augmente pour générer une prédiction.
La seconde limite est de nature plus fondamentale. Les diagrammes de Feyman se basent sur la supposition que la quantité des collisions et des sous-collisions sera proportionnelle à la précision de leurs prédictions. Ce processus de calcul, connu comme l’expansion perturbative, fonctionne bien pour les collisions de particules d’électrons où la force nucléaire faible et électromagnétique dominent. Mais elle fonctionne moins bien pour les collisions à haute énergie comme les collisions entre des protons où c’est la force nucléaire forte qui va dominer. Dans ces cas, le comptage pour une grande quantité de collisions, en dessinant des diagrammes de Feynman plus élaborés, a tendance à égarer les physiciens. On sait que cela commence à diverger à partir d’un certain point selon Francis Brow, un mathématicien de l’université d’Oxford, mais on ignore comment estimer le point où nous devons arrêter de calculer les diagrammes.
Mais il y a des raisons d’espérer. Cette dernière décennie, les physiciens et les mathématiciens ont commencé à exploiter une correspondance surprenante qui pourrait donner une seconde vie aux vénérables diagrammes de Feynman et proposer des indices en mathématique et en physique. Cela concerne un fait étrange que des valeurs calculées par les diagrammes de Feynman semblent correspondre parfaitement à des nombres importants qui apparaissent dans une branche des mathématiques connue comme la géométrie algébrique.1 On connait ces valeurs comme des périodes de motifs et il n’y a aucune raison sur le fait que ces valeurs doivent apparaitre dans les 2 configurations. C’est aussi étrange qu’à chaque fois que vous mesuriez un bol de riz, vous observiez que la quantité de graines est toujours un nombre premier. Il y a une connexion naturelle vers la géométrie algébrique et les périodes et avec le recul, ce n’est pas une coïncidence selon Dirk Kreimer, un physicien à l’université de Humboldt à Berlin.
Désormais, les mathématiciens et les physiciens travaillent ensemble pour comprendre cette coïncidence. Pour les mathématiciens, les physiciens ont porté leur attention sur une classe spéciale de nombres qu’ils voudraient comprendre. Est-ce qu’il y a une structure cachée à ces périodes qui se produisent en physique ? Quelles sont les propriétés spéciales que cette classe de nombres pourrait avoir ? Pour les physiciens, la récompense de cette compréhension mathématique proposera un nouveau degré de clairvoyance quand il s’agit de prédire le monde quantique de nature “chaotique”.
Sommaire
Un thème récurrent
Aujourd’hui, les périodes (ou fonction périodique) sont les sujets les plus abstraits des mathématiques, mais ils ont commencé pour résoudre des problèmes plus concrets.2 Au début du 17e siècle, les scientifiques comme Galileo Galilei étaient intéressés sur comment calculer la longueur de temps d’un balancier pour faire un tour complet. Ils ont réalisé que le calcul se réduisait à prendre une intégrale, un genre de somme infinie, d’une fonction qui combinait l’information sur la longueur et l’angle de libération de la pendule. À la même époque, Johannes Kepler a utilisé des calculs similaires pour établir la durée pour qu’une planète tourne autour du soleil. Ces différents scientifiques ont appelé ces mesures comme des périodes et ils ont fait en sorte qu’ils soient les mesures les plus importantes sur le mouvement.
Au 18e et 19e siècle, les mathématiciens se sont mis à étudier les périodes de manière plus générale et non liée simplement à des balanciers ou des planètes. L’étude concernait une classe de nombres générée en intégrant des fonctions polynomiales telles que x2 + 2x – 6 et 3x3 – 4x2 – 2x + 6. Pendant plus d’un siècle, des sommités comme Carl Friedrich Gauss et Leonhard Euler ont exploré l’univers des périodes et ils ont trouvé qu’ils contenaient de nombreuses caractéristiques qui pointent vers un ordre sous-jacent. Dans un sens, la géométrie algébrique, qui étudie les formes géométriques des équations polynomiales, a été développée au 20e siècle comme un moyen de poursuivre cette structure cachée.
Ces efforts ont rapidement progressé en 1960. À cette époque, les mathématiciens avaient fait ce qu’ils ont l’habitude de faire, à savoir, transformer des objets relativement concrets en des équations plus abstraites. Pour eux, cela devrait permettre d’identifier des relations qui ne semblent pas apparentes. En premier lieu, ce processus a impliqué de regarder des objets géométriques (connus comme des variétés algébriques) définis par les solutions aux classes des fonctions polynomiales plutôt que de regarder directement les fonctions. Ensuite, les mathématiciens ont tenté de comprendre les propriétés basiques de ces objets géométriques. Pour le faire, ils ont développé ce qu’on connait comme les théories de cohomologie qui sont des manières d’identifier des aspects structurels d’objets géométriques qui sont les mêmes indépendamment de l’équation polynomiale qui a été utilisée pour générer les objets.3 4
À partir des années 1960, les théories de cohomologie ont proliféré dans tous les sens pour nous donner la cohomologie singulière, la cohomologie de Rham, la cohomologie étale, etc. Chacune semblait avoir une vision différente sur les caractéristiques importantes des variétés algébriques. C’est dans ce paysage dispersé qu’Alexander Grothendieck, mort en 2014, a réalisé que toutes les théories de cohomologie étaient des versions différentes de la même chose. Grothendieck a observé que dans le cas de la variété algébrique, indépendamment de la manière dont vous calculez ces différentes théories de cohomologie, vous aurez plus ou moins la même réponse selon Brown.
Cette réponse identique, la seule chose au centre de toutes les théories de cohomologie, était ce que Grothendieck avait appelé un motif. En musique, un motif est un thème récurrent. Pour Grothendieck, un motif est quelque chose qui va revenir encore et encore sous différentes formes, mais c’est la même chose selon Pierre Cartier, un mathématicien à l’Institut des hautes études scientifiques (IHÉS) à côté de Paris et un ancien collègue de Grothendieck.
Dans ce sens, les motifs sont des briques élémentaires des équations polynomiales de la même manière que les nombres premiers sont les briques élémentaires de nombres plus grands. Les motifs ont aussi leurs propres données qui leur sont associées. De la même manière que vous fractionnez la matière en des éléments pour spécifier les caractéristiques de chaque élément tel que son nombre ou poids atomique, les mathématiciens attribuent des mesures essentielles à un motif. Et l’une des mesures les plus importantes est les périodes de motifs. Et si la période d’un motif, se produisant dans un système d’équations polynomiales, est la même que la période d’un motif se produisant dans un autre système, alors vous savez que les motifs sont les mêmes. Une fois que vous connaissez les périodes, qui sont des nombres spécifiques, c’est quasiment la même chose que de connaitre le motif proprement dit selon Minhyong Kim, un mathématicien à Oxford.
Un moyen direct de voir la même période qui apparait dans des contextes inattendus est la valeur Pi. C’est l’exemple le plus célèbre pour obtenir une période selon Cartier. Pi apparait sous de nombreuses apparences en géométrie : Dans l’intégrale de la fonction qui définit un cercle à une dimension, dans l’intégrale d’une fonction qui définit un cercle à deux dimensions et dans l’intégrale de la fonction qui définit une sphère. Qu’une valeur identique comme Pi apparaisse dans des intégrales très différentes semblait mystérieux aux anciens penseurs. L’explication moderne est que la sphère et le cercle solide ont le même motif et donc, ils ont la même période selon Brown.
Le chemin difficile de Feynman
Si des esprits curieux voulaient savoir pourquoi des valeurs comme Pi apparaissaient dans des calculs sur le cercle et la sphère, les mathématiciens et les physiciens d’aujourd’hui voudraient savoir pourquoi ces valeurs apparaissent dans des objets géométriques différents que sont les diagrammes de Feynman.
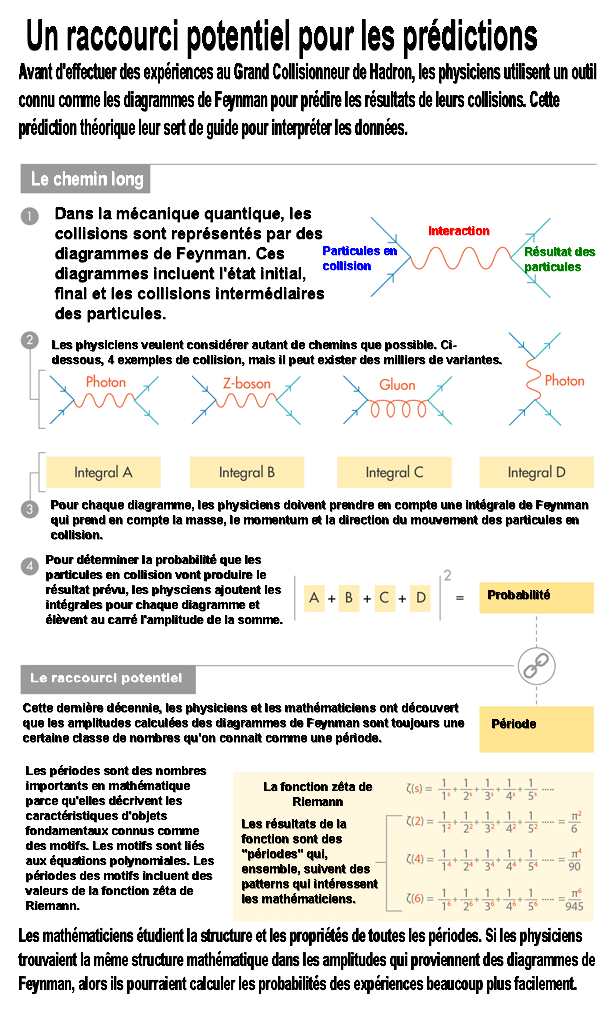
Les diagrammes de Feynman ont un aspect géométrique assez basique, car ils sont formés par des segments de ligne, de rayons et de vertex. Pour voir leur construction et pourquoi sont-ils utiles en physique, imaginez une simple expérience où un électron et un positron se percutent pour produire un muon et un antimuon. Pour calculer la probabilité du résultat, un physicien devra connaitre la masse et le momentum de chaque particule et des indices sur le chemin que la particule a suivi. En mécanique quantique, le chemin qu’une particule peut prendre est considéré comme la moyenne de tous ses chemins possibles. Le calcul de ce chemin revient à prendre une intégrale, connue comme une intégrale de chemin de Feynman, sur l’ensemble des chemins.5
Chaque route qu’une collision de particule peut prendre du début jusqu’à la fin peut être représentée par un diagramme de Feynman et chaque diagramme possède sa propre intégrale (le diagramme et son intégrale sont les mêmes). Pour calculer la probabilité d’un résultat spécifique sur ce qui va se produire, prenez chaque intégrale et ajoutez-les ensemble. Ce nombre est l’amplitude du diagramme. Les physiciens vont élever au carré la magnitude de ce nombre pour avoir la probabilité.
Cette procédure est facile pour un électron et un positron qui vont produire un muon et un antimuon. Mais c’est de la physique assez “barbante”. Les expériences qui intéressent vraiment les physiciens concernent celles qui impliquent des diagrammes de Feynman avec des boucles. Les boucles représentent des situations dans lesquelles les particules émettent et réabsorbent des particules supplémentaires. Quand un électron percute un positron, il y a un nombre infini de collisions intermédiaires qui peuvent se produire avant que la paire finale de muon et d’antimuon apparaisse. Dans ces collisions intermédiaires, les nouvelles particules comme des photons sont créées et détruites avant qu’on puisse les observer. Les particules entrantes et sortantes sont les mêmes que décrites précédemment, mais le fait est que ces collisions non observables peuvent toujours provoquer des effets subtils sur le résultat. C’est comme un Tinkertoys. Une fois que vous dessinez un diagramme, vous connectez plus de lignes selon les règles de la théorie selon Flip Tanedo, un physicien de l’université de Californie. Vous pouvez connecter plus de baguettes et de noeuds pour compliquer les choses.
En considérant les boucles, les physiciens augmentent la précision de leurs expériences. L’ajout d’une boucle est comme calculer une valeur vers une quantité plus grande de décimales. Mais à chaque fois qu’on ajoute une boucle, la quantité de diagrammes de Feynman doit être reconsidérée et la difficulté des intégrales correspondantes augmente de manière dramatique. Par exemple, un système simple à une boucle nécessite un seul diagramme. Une version à 2 boucles nécessite 7 diagrammes. 3 boucles nécessitent 72 diagrammes. Et si vous avez 5 boucles, alors le calcul nécessite 12 000 intégrales et c’est un calcul informatique qui peut prendre des années. Plutôt que de se plonger dans de nombreuses intégrales, les physiciens aimeraient avoir un sens de l’amplitude finale en regardant la structure d’un diagramme de Feyman de la même manière que les mathématiciens peuvent associer les périodes avec les motifs. Cette procédure est si complexe et les intégrales sont tellement difficiles que les physiciens veulent des indices sur la réponse finale, que ce soit l’intégrale ou la période, en regardant simplement le graphique selon Brown.
Une connexion surprenante
Les périodes et les amplitudes ont été présentées ensemble pour la première fois en 1994 par Kreimer et David Broadhurst, un physicien à l’Open University en Angleterre avec un papier qui a suivi en 1995.6 Ces travaux ont mené les mathématiciens à spéculer que toutes les amplitudes étaient des périodes de motifs mélangées de Tate. Le motif de Tate a été nommé d’après John Tate, un professeur émérite à l’université d’Harvard dans lequel toutes les périodes sont des valeurs multiples d’une des constructions les plus influentes dans la théorie des nombres qui est la fonction zêta de Riemann.7 Dans la situation de la paire électron/positron et du résultat de muon/antimuon, la principale partie de l’amplitude est sortie 6 fois par rapport à la fonction zêta de Riemann.
Si toutes les amplitudes étaient des valeurs zêta multiples, alors cela permettrait aux physiciens de travailler avec une classe de nombres bien définie. Mais en 2012, Brown et son collaborateur Oliver Schnetz ont prouvé que ce n’était pas le cas.8 Même si toutes les amplitudes actuelles peuvent être des périodes de motifs mélangés de Tate, il y a des monstres tapis dans l’ombre qui jettent une clé à molette dans la machine selon Brown. Ces monstres sont certainement des périodes, mais ce ne sont pas les périodes simples et “gentilles” que les gens espéraient.
Les mathématiciens et les physiciens savent qu’il y a connexion entre le nombre de boucles dans un diagramme de Feyman et une notion connue comme le poids en mathématique. Le poids est un nombre associé à la dimension de l’espace qui est intégré. Une intégrale de période sur un espace à 1 dimension peut avoir un poids de 0, 1 ou 2, une intégrale de période sur un espace à 2 dimensions peut avoir un poids jusqu’à 4, etc. On peut aussi utiliser le poids pour tirer les périodes en différents types : Toutes les périodes d’un poids de 0 sont conjecturées comme des nombres algébriques qui peuvent être des solutions à des équations polynomiales (ce qui n’a pas encore été prouvé), la période d’un balancier aura toujours un poids de 1, Pi est une période avec un poids de 2 et les poids des valeurs de la fonction zêta de Riemann sont toujours le double de l’entrée (donc, la fonction de zêta évalué à 3 aura toujours un poids de 6).
Cette classification des périodes par les poids se transpose sur les diagrammes de Feynman où le nombre de boucles dans un diagramme est plus ou moins associé au poids de son amplitude. Les diagrammes sans boucle ont un poids de 0, les amplitudes de diagramme avec 1 boucle sont toutes les périodes de motifs mélangés de Tate et elles possèdent un poids maximal de 4. Pour des graphiques avec des boucles supplémentaires, les mathématiciens estiment que la relation continue même s’ils ne peuvent pas encore la voir. Nous allons vers des boucles élevées et nous voyons des périodes d’un type plus général selon Kreimer. Il y a des mathématiciens qui sont vraiment intéressés parce qu’ils ne comprennent pas les motifs qui ne sont pas des motifs mélangés de Tate.
Les mathématiciens et les physiciens font actuellement des va-et-vient pour établir l’ampleur du problème et proposer des solutions. Les mathématiciens suggèrent des fonctions (et leurs intégrales) aux physiciens qu’ils peuvent utiliser pour décrire des diagrammes de Feynman. Les physiciens produisent des configurations de collisions de particules qui surpassent les fonctions offertes par les mathématiciens. Il est étonnant de voir qu’ils ont assimilé rapidement des idées mathématiques très techniques selon Brown. Nous sommes à court de nombres et de fonctions classiques qu’on pourrait leur donner.
Les groupes de la nature
Depuis le développement du calcul au 17e siècle, les nombres qui apparaissent dans le monde physique ont influencé le progrès mathématique. Et c’est encore le cas aujourd’hui. Le fait que les périodes, qui viennent de la physique en étant dans un sens “données par la nature” et les théories physiques, possèdent de nombreuses structures et c’est une structure qu’un mathématicien ne penserait pas à chercher ou à inventer selon Brown. Et pour Kreimer, il semble que les périodes voulues par la nature sont un ensemble plus petit que les périodes qui peuvent être définis en mathématique, mais nous ne pouvons pas définir correctement ce sous-ensemble.
Brown cherche à prouver qu’il y a un groupe mathématique, connu comme le groupe de Galois, qui agit sur l’ensemble des périodes provenant des diagrammes de Feynman. La réponse semble oui à chaque fois qu’on fait le calcul, mais la preuve que la relation se maintienne est une autre histoire. Si c’est vrai qu’il y a un groupe qui agit sur les nombres provenant de la physique, alors cela signifie que vous trouverez une grande classe de symétries selon Brown. Et si c’est le cas, alors la prochaine étape est de chercher la raison de ce groupe de symétrie et qu’est-ce que cela signifie pour la physique.
Entre autres, cela approfondirait la relation qui est déjà provocante entre les constructions géométriques fondamentales provenant de 2 contextes très différents : Les motifs, les objets que les mathématiciens ont conçus il y a 50 ans pour comprendre les solutions aux équations polynomiales et les diagrammes de Feynman, la représentation schématique des collisions de particule. Chaque diagramme de Feynman possède un motif qui lui est attaché. Mais il reste à déterminer ce que la structure d’un motif nous dit sur la structure de ce diagramme associé.









Passionnant.
On pourrait aussi imaginer un développement sur le mode de l’entendement comme extension de l’écoute. Or il n’y a pas que la sonorité qui stimule une perception: il y a aussi la visualité. Et la touchabilité…etc.
Donc on peut envisager l’entendement du visuel, l’entendement du toucher, …etc.
Au fond il n’y a pas de théorie construite de sa subjectivité propre au regard de l’exploration et de l’expérimentation objective, sauf le passage obligé par les trous du corps et leurs bords érogènes.
Cette théorie qui renvoie au sujet qui est représenté (par un signifiant pour un autre signifiant) sup-pose une Autre abstrait référentiel.
Rien que de le dire on mesure l’hénaurme béance face aux recherches mathématiques: le motif du retrait de G par exemple nous secoue devant ce qui est en jeu dans le sujet-de-le-parole (y compris mathématicien depuis l’invention de l’écriture il y a +ou- 5000 ans après 2 millions d’années à prendre le réel dans le nez !)